Evelyn B. Christensen - Author & Puzzle Creator

A Handy Multiplication Mystery

By Evelyn B. Christensen and Stephen M. Christensen

We had finished the Thanksgiving meal and several of us were relaxing on the front porch. I sat on the swing next to my 8-year-old niece. "What interesting things have you been learning in school recently, Ya'el?"

She told me she'd been learning her multiplication tables. As a former math teacher and elementary teacher I was pleased she considered that interesting. I asked her if she was familiar with the trick of doing the nines table on her fingers. Yep, she knew that one. Then I asked her if she knew about doing the higher facts for 6s up through 10s on her fingers. She hadn't heard about that trick so I explained it to her.

Turn your hands palm up toward you. Assign the number 6 to your thumbs, 7 to your index fingers, ..., 10 to your pinkies.

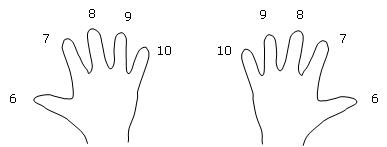
Choose a multiplication problem so that both factors are a number 6-10. Touch together the two fingers with those assigned numbers. Count the number of fingers that are between you and the touching fingers, including the two touching fingers. You have that many 10s. Now multiply the number of left-hand fingers beyond the touching fingers times the number of right-hand fingers beyond the touching fingers, and add the product to your first number. That gives you the answer to your multiplication problem.

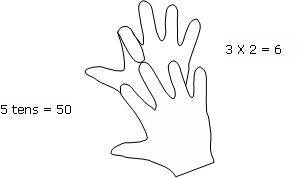
Here's an example: multiply 7 times 8. Touch your left pointer finger to your right middle finger. Including the touching fingers, you have five fingers between you and those fingers. That gives you 5 tens or 50. You have 3 left-hand fingers beyond the touching fingers and 2 right-hand fingers. 3 X 2 = 6. Add that to the 50, and you have 56, which is the answer to 7 X 8.

I demonstrated several more examples. "I think that trick's pretty amazing!" I concluded. "I only learned it two or three years ago myself, and I have no idea why it works."

Others on the porch had been listening and agreed it was really cool. My son Stephen said, "There's got to be a mathematical reason for it. I'm going to figure out why it works." He went inside to get paper and pencil from Aunt Marilyn.

After a while he came back out triumphantly. He had actually solved the mystery! He showed me the sheet with his calculations:

6 7 8 9 10 factors being multiplied

X = 1 2 3 4   5   left hand fingers

Y = 1 2 3 4   5   right hand fingers

   Let X be 5 less than the left hand factor we're multiplying.

   Let Y be 5 less than the right hand factor we're multiplying.

   For the formula, our fingers are now numbered 1-5,

         instead of 6-10.

   Formula: 10X + 10Y + (5 - X)(5 - Y) = Answer

   Example: if we're doing 8 x 6, then X = 3 and Y = 1

      10(3) + 10(1) + (5 - 3)(5 - 1) = 48

   Why it works: 10X + 10Y + (5 - X)(5 - Y) = Answer

      10X + 10Y + 25 - 5X - 5Y + XY = Answer

      25 + 5X + 5Y + XY = Answer

      (5 + X)(5 + Y) = Answer

   We originally assigned X and Y to be 5 less than the numbers we were multiplying, so our formula takes that into account.

Wow! Some simple algebra, but who would have guessed!

Stephen said that Uncle Bill had wondered if the process would work for other bases.

"I don't understand what you mean," I said.

Stephen gave me an example. Suppose you only have 8 fingers instead of 10. For the sake of illustration, don't use your thumbs. Then the other fingers are numbered 5_eight, 6_eight, 7_eight, and 10_eight. Try 6_eight x 7_eight. Touch those fingers together. We have five 10_eight front fingers + (1_eight x 2_eight) with the back fingers. That gives 52_eight which equals 42_ten. So it works for that example.

Does it work for every example in base 8? Can you prove it mathematically?

How about for base 12? (You might need a friend to provide those extra two fingers.)

Does it work for all bases? If not, which ones don't work?

Perhaps your students would like to explore some of these questions, as well as the original mystery question which Stephen solved. Clearly, our family had our fingers in an interesting "pie" that Thanksgiving and managed to pull out some fun mathematical plums! Your students might find them fun, too.

This is a pre-publication version of “A Handy Multiplication Mystery,” Mathematics Teaching in the Middle School, Vol. 17, No. 1, 2011. Copyright 2011. Used with permission from the National Council of Teachers of Mathematics. All rights reserved.