|








|
|
|
A Discovery Adventure with Multiplication Facts
For me, the numbers 1-9 have always had personalities, but over the years I've come to realize that this
isn't a common way of thinking about them. I suppose that somewhere back in my early mathematical
experiences, when the whole thing with numbers was very boring, this anthropomorphic approach gave them
some interest.
I don't make a habit of discussing the personalities of numbers with other people; however, recently I
found it useful when helping my 7-year-old son practice his multiplication facts. Stephen understands the
concepts and can figure out answers given enough time, but we were working on fast recall. He was having
trouble with the higher numbers, so when he was stuck on 7x7, I said, "Try thinking about it this way: 7
really wishes he could be big and important. He'd like to reach at least halfway to 100, but you
know what? He never can by himself. No matter how hard he tries he always falls one short. What do you
suppose 7x7 is?"
His face lighting up, he grinned and promptly said, "49!" He hasn't missed 7x7 since. Number Seven's
personality helped him to fashion his own useful "memory hook."
But the story doesn't end there. While 7x7 no longer gave Stephen trouble, 6x8 did. So I tried relating
it to 49: "You already know 7x7 is 49. Just remember that 6 and 8 come on either side of 7. Their product
is 1 less than the 7's." That seemed a feasible mnemonic device for him, so, as we rode along in the car,
we went on to 4x6.
He thought for a few seconds and then said triumphantly, "24!"
I could tell that he hadn't spent time counting up by 4's or 6's, and since I'm always interested in the
process of mathematical thinking, I asked him how he got his answer. His response made me do a mental
retake.
"Well," he said, "5x5 is 25 and since 4 and 6 are on either side of 5, the answer is 24."
He was absolutely right, of course, but was this just a coincidence? My "6x8 is 1 less than 7x7" was
offered as a catchy way to remember a number and not intended as a rule. We checked some other examples,
using odd numbers (assuming the pattern was applicable only to those because the first two squares that
worked for us were odd), and by the time we reached our destination and had to stop, we'd verified our
new rule for odd squares under 10.
The next afternoon, once again in the car, we resumed our figuring, and it didn't take us long to branch
out into even numbers. With each new example we tested and found fit our rule, our excitement grew. By
the time we picked up his older sister at middle school, Stephen was bursting with excitement and begged
me to let him be the one to tell Susan about our discovery.
As soon as he explained it to her, she immediately began testing her own examples beyond 100. "Yep! It
works for 11. 11x11 is 121 and 10x12 is 120. What's 12x14?"
I had to figure for a minute. "168."
"Yep! It works for numbers as big as 13 squared." She was off and running with this new idea. "It even
works for 1 and 0. You know, sometimes a rule will work for everything else, but won't for one of those."
By this time, of course, the next logical step was to figure out algebraically why this pattern worked.
Susan is taking algebra, so I said to her, "We've got a number x and we're multiplying (x-1) times (x+1).
What does that give us?" The answer was immediate and obvious to both of us. "x2-1. Of
course, the rule is going to work for every example!"
Such an obvious bit of algebra. Why hadn't we realized it? But how often is algebra used to learn basic
multiplication facts? It was a new and different and exciting experience for all three of us. Perhaps
the most exciting part was our discovering a relationship other students could use in learning some of
their multiplication facts.
But, still, we weren't quite finished. The algebra equation had naturally provided a satisfactory sense
of completion for my seventh grader, but I wanted to be sure that Stephen understood why this relationship
worked. A set of square tiles made this possible. We built a 7x7 array. Then Stephen slid
the tiles around to make 6x8 and saw that there was one tile left over. He built lots of other examples,
always with one extra tile left; visually now, this new rule made sense. (Perhaps, on another day, we'll
even try an extension. What happens if instead of taking numbers that are 1 more and 1 less than 7, we
try ones that are 2 more and 2 less?)
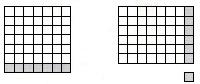
7 x 7 6 x 8
When I was Stephen's age, I thought math was boring. Clearly, it doesn't have to be! Creativity and the
excitement of shared discovery are precious gifts; Stephen would recommend them for any child you know.
Understanding Our Gifted, May/June, 1995. Reprinted with Permission, Open Space Communications LLC. 800-494-6178 /
www.openspacecomm.com.
|
|
|
|
