|








|
|
|
Finding Averages with Building Blocks
Objective
Students use wooden cubes to find the averages of given sets of numbers.
Materials
Approximately 25 wooden cubes for each student (or for each pair, if working together).
Copies of "Averaging" problem sheets, mounted on card stock, and laminated. (See figures 1-3 for examples. These would need to be enlarged.)
Copies of "Finding Averages" answer sheets. (See figure 4.)
Layout cards for the towers. (See figure 5. Not all students will want to use them, but they're helpful for sets of numbers
involving zero.)
Directions
Introduce the concept of averages with the following story. As you begin to tell students the story, randomly
build cube towers these heights: 2,3,3,3,3,4,4,4,5,5,5,5,6.
|
|
Suppose I have a kid sister who's about one and a half years old and I look over one day and notice that she's
building towers with her blocks. Since she's never done this before, this is a big accomplishment. I'm so
excited that she's learned to do this that I call up by best friend Juan and say, "Guess what, Juan! Lara's
learned to build towers with her blocks! It's really exciting. She's sitting here building lots and lots of them."
Now Juan wants to be a good friend, so he says, "Wow! That's wonderful! How tall is she building them?"
What am I going to tell him? If I say, "Well, she built one that's 6 blocks high," will that give him a very
accurate picture of what she's doing? Maybe I could say, "Let's see. She's built one that's 5 blocks, one that's
3, one that's 2, another that's 2, one that's 6, one that's 4, another that's 4, one that's 3,...." [Continue
pointing to various towers and giving the number.] Will Juan be able to make much sense of a list of all those
numbers given like that?
What we need is a way for me to give Juan one number that will be a good representative of all the towers
Lara has built. Let's see if there's some way we can sort of balance out these towers. Here's a 6-block tower
and a 2-block one. We could take these 2 blocks from the six and add them to the two.
[Continue the process of "averaging" the taller towers with the shorter towers until all the towers are four
blocks high.] What do you think would be a good number to tell Juan for the height of Lara's towers? Right! We
could say, "Well, she's building some higher and some lower, but they're about four blocks high."
What we just did is called 'finding the average' of the height of all those different towers. If we have a whole
list of numbers and want to find just one number to represent all of them, we can find the average.
|
|
Give out problem cards and blocks and let students begin finding the averages. Stress that once they've built
their initial towers for a problem, they can't take any more blocks from their stockpiles to balance them. Have
them record their original towers and the average on the answer sheets.
Follow-up activity
Once the students feel confident in finding averages with the picture problem cards, make
problem cards that just give the numbers. Example: Find the average of 5, 1, 7, and 11. Continue to make the
blocks available for them to use in solving the problems.
|
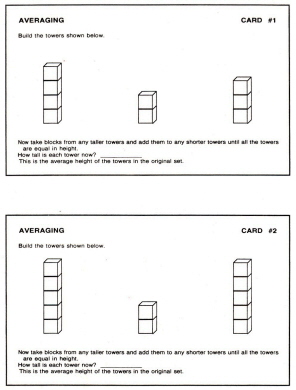
Figure 1
|
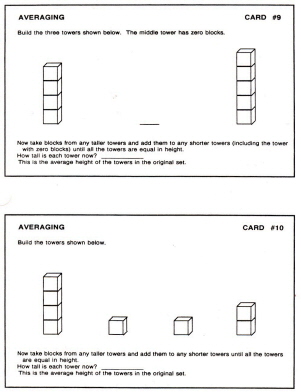
Figure 2
|
|
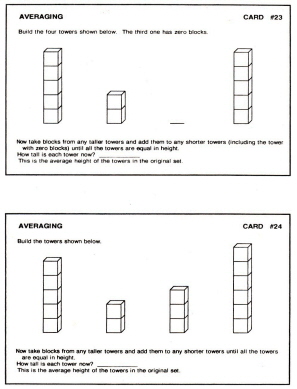
Figure 3
|
|
|
|
|
|
